あるバラエティー番組の外見だけでT大生を当てるというコーナーで,
T大生かどうかを次の様な計算させて確認するというのがあった.
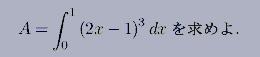 これはいわゆる定積分というもので, 高校で数学を学んだ人にとっては
内容はともかくどこかで必ず見たことはあるであろう.
この手の定積分の問題は公式をあてはめて,以下の様に計算することにより,
答えである0を求めることが出来る.
これはいわゆる定積分というもので, 高校で数学を学んだ人にとっては
内容はともかくどこかで必ず見たことはあるであろう.
この手の定積分の問題は公式をあてはめて,以下の様に計算することにより,
答えである0を求めることが出来る.
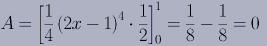 番組のコーナーは, 計算が出来た人がT大生だとわかった時点で終わったのだが,
実際の教育現場でもこのような方法, つまり, ただ単に公式を当てはめて答えが合えば正解,
それで終わりという指導方法に偏りすぎている傾向があるのではないか?
数学的背景にあるイメージというのがないがしろにされているような気がする.
この問題で言うと, 定積分のイメージ(数学用語の像(イメージ)ではない)は面積である.
番組のコーナーは, 計算が出来た人がT大生だとわかった時点で終わったのだが,
実際の教育現場でもこのような方法, つまり, ただ単に公式を当てはめて答えが合えば正解,
それで終わりという指導方法に偏りすぎている傾向があるのではないか?
数学的背景にあるイメージというのがないがしろにされているような気がする.
この問題で言うと, 定積分のイメージ(数学用語の像(イメージ)ではない)は面積である.
ある難しい計算をして答えが0になったら, そこには必ず「何故?」という疑問が生じるはずである.
この問題をイメージで考えてみよう.
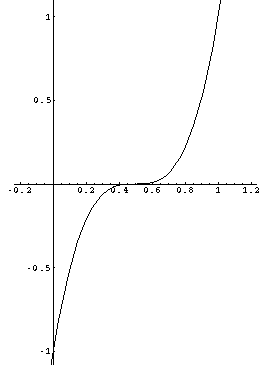
まず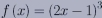 とおくとおくと,
とおくとおくと, 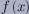 のグラフは次のようになる.
のグラフは次のようになる.
 グラフを描くためには
グラフを描くためには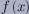 を
を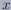 で微分して, 導関数の符号から
で微分して, 導関数の符号から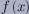 の増減を調べればよいが,
計算をしなくとも
の増減を調べればよいが,
計算をしなくとも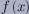 は,
は,  のグラフを
のグラフを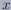 軸方向に
軸方向に 平行移動させたものであるから, 極値を持たず,
平行移動させたものであるから, 極値を持たず,
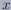 軸上の
軸上の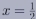 で変曲点を持つ上のグラフがイメージ出来るであろう.ここで,
で変曲点を持つ上のグラフがイメージ出来るであろう.ここで, 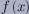 を
を
 から
から まで積分するということは, グラフで考えると
まで積分するということは, グラフで考えると
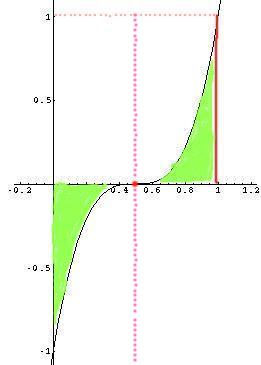 の部分の面積を求めるということと同値である.ただし,
の部分の面積を求めるということと同値である.ただし,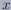 軸の下の面積は
マイナスの値であることに注意をしなければならない.ここで
軸の下の面積は
マイナスの値であることに注意をしなければならない.ここで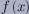 は
は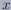 軸上の
軸上の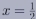 なる点に関して点対称であるから,
それぞれの面積は絶対値が同じで符号だけ違うので, 相殺し合い, 結果として0になることが
"イメージ"としてわかる.結局, 計算を全くしなくてもイメージだけで答えが0になることが
わかるのである.
なる点に関して点対称であるから,
それぞれの面積は絶対値が同じで符号だけ違うので, 相殺し合い, 結果として0になることが
"イメージ"としてわかる.結局, 計算を全くしなくてもイメージだけで答えが0になることが
わかるのである.
実際は, 計算結果を見てから初めて面積に着目することに気付く場合が普通だろう.ただ重要なのは「計算出来ました.はい終わりです.」なのではなく,
「計算結果が0になったのは何故か?」,「数学的背景にはどういう現象が起きているのか?」といった探求心を持つことであり,
問題の背景をイメージでとらえることが大事なことである.
現在の数学教育では,数学的対象をイメージとしてとらえる訓練があまり行われていないので,
今日のいわゆる"数学嫌い"が深刻化しているのではないだろうか.
人間には本来, 未知なる物に対する
探求心を必ず持っているはずである.そしてイメージというのはその探求心をかき立てるのに
最適なツールとなるはずであるである.
探求心を最大限に活かせる数学教育を望みたい.
戻る
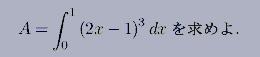
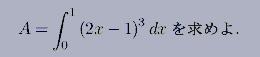
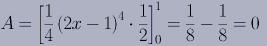
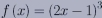 とおくとおくと,
とおくとおくと, 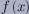 のグラフは次のようになる.
のグラフは次のようになる.

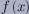 を
を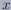 で微分して, 導関数の符号から
で微分して, 導関数の符号から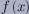 の増減を調べればよいが,
計算をしなくとも
の増減を調べればよいが,
計算をしなくとも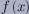 は,
は,  のグラフを
のグラフを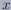 軸方向に
軸方向に 平行移動させたものであるから, 極値を持たず,
平行移動させたものであるから, 極値を持たず,
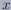 軸上の
軸上の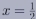 で変曲点を持つ上のグラフがイメージ出来るであろう.ここで,
で変曲点を持つ上のグラフがイメージ出来るであろう.ここで, 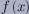 を
を
 から
から まで積分するということは, グラフで考えると
まで積分するということは, グラフで考えると

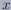 軸の下の面積は
マイナスの値であることに注意をしなければならない.ここで
軸の下の面積は
マイナスの値であることに注意をしなければならない.ここで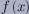 は
は 軸上の
軸上の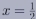 なる点に関して点対称であるから,
それぞれの面積は絶対値が同じで符号だけ違うので, 相殺し合い, 結果として0になることが
"イメージ"としてわかる.結局, 計算を全くしなくてもイメージだけで答えが0になることが
わかるのである.
なる点に関して点対称であるから,
それぞれの面積は絶対値が同じで符号だけ違うので, 相殺し合い, 結果として0になることが
"イメージ"としてわかる.結局, 計算を全くしなくてもイメージだけで答えが0になることが
わかるのである.